29Комплексные числа

Мы начинали курс с обсуждения чисел, ими же и закончим. Всё началось с натуральных чисел. Натуральные числа можно складывать, умножать и возводить в степени, но не всегда можно вычитать. Попробуйте-ка вычесть пять из трёх — если вам известны только натуральные числа, не получится. Приходится изобретать отрицательные. С отрицательными числами вычитание работает без проблем, но с делением есть трудности — четыре на два поделятся, а на три — нет. Рациональные числа лишены этой проблемы: делить можно что угодно на что угодно, кроме нуля (с нулём так всегда будет, тут уж ничего не поделать). Однако, корни извлекать не всегда получается — например, корень из двух не является рациональным числом. Чтобы эту проблему решить, придумали вещественные числа. Теперь корни извлекаются — но только из неотрицательных чисел. А что делать, если очень хочется извлечь корень из отрицательного числа? Как обычно — придумывать новые числа!

29.1Построение комплексных чисел

29.1.1Мнимая единица

Когда мы не смогли поделить четыре на три, мы сказали — ну и ладно, давайте просто объявим, что $4/3$ — это новое число — не натуральное и не целое, но рациональное. Потом мы придумали две вещи: во-первых, как вложить множество целых чисел в множество рациональных — мы знаем, что целое число $3$ — это то же самое, что рациональное число $3/1$. Во-вторых, как рациональные числа складывать и умножать.

С корнями из отрицательных чисел можно поступить аналогично. Допустим, очень хочется вычислить квадратный корень из минус единицы. Давайте считать, что мы его вычислили, и обозначим результат через $i$. Эта штука называется мнимой единицей. Мы бы хотели извлекать квадратный корень не только из минус единицы, но и из других отрицательных чисел. Однако, как мы скоро увидим, ничего специального для этого делать не придётся.

Конечно, $i$ не является вещественным числом, поскольку мы хорошо знаем, что квадрат любого вещественного числа неотрицателен (ну вот просто так мы определили операции — минус на минус даёт плюс, поэтому отрицательного ничего не получится). Тем не менее, давайте считать, что это всё-таки число — какого-то нового, невиданного доселе типа — и что его можно включать в арифметические операции.

Самое главное (и, по большому счёту, единственное), что мы знаем про $i$ и арифметические операции — что если его умножить на себя, то получится минус единица:

Взаимодействие $i$ с вещественными числами определим самым простым образом: никак. То есть выражение, например, $(2+3i)$ никак нельзя упростить — это просто запись одного из наших новых чисел. Когда мы придумали рациональные числа, у каждого такого числа оказалось две части — числитель и знаменатель, оба относились к ранее определенным классам чисел — целым и натуральным. А у комплексных чисел тоже две части, одна без $i$, а другая с $i$.

Итак, по определению, множество комплексных чисел — это множество

Пусть $z=x+iy$ — какое-то комплексное число. Тогда $x$ называется его вещественной частью (real), а $y$ — мнимой (imaginary). Обозначаются: Заметим, что $x$ и $y$ — вещественные числа. Всю комплексную магию добавляет число $i$.

29.1.2Арифметические операции с комплексными числами

В дальнейшем мы будем предполагать, что привычные для нас правила работы с числами — например, «от перестановки слагаемых сумма не меняется» и т.д. сохраняются и в случае комплексных чисел — по крайней мере, до тех пор, пока это возможно.

Сложение. Пусть $z_1=x_1+i{y}_1$ и $z_2=x_2+i{y}_2$ — два комплексных числа. Их сумма определяется так:

Я воспользовался стандартными правилами — про перестановку слагаемых и про вынесение за скобку. Таким образом, чтобы сложить два комплексных числа, нужно сложить их вещественные и мнимые части по отдельности.

Умножение. Тут будет посложнее.

Коммутативность умножения, в которую мы по-прежнему верим, позволяет сказать, что $x_{1}i{y}_2=i{x}_1{y}_2$ и $i{y}_{1}i{y}_2=i\cdot i{y}_1{y}_2=i^2{y}_1{y}_2$. Но мы знаем, что $i^2=-1$, и значит получается $-y_1{y}_2$. Итак: Формула не самая короткая, и сходу даже непонятно, какие свойства у этой операции. Например, точно ли выполняется ассоциативность ($\left(z_1{z}_2\right)z_3=z_1\left(z_2{z}_3\right)$), как сложение взаимодействует с умножением и т.д. — всё это надо проверять (спойлер: всё работает). Чуть попозже мы обсудим, как умножение записывать короче и как правильно о нём думать.

29.1.3Комплексная плоскость

Всякие комплексное число задаётся парой вещественных чисел — действительной и мнимой частью. С другой стороны, мы знаем, что парами вещественных чисел задаются точки на плоскости. Каждой точке можно также сопоставить радиус-вектор — стрелочку, которая начинается в нуле, а заканчивается в этой точке. (Эту стрелочку также можно переносить по всей плоскости, сохраняя направление и длину — иногда бывает полезно откладывать вектор не от нуля, а от другой точки.) Мы будем думать про комплексные числа как про такие векторы. Точка $(1,0)$ и её радиус-вектор соответствуют вещественному числу $1$, а точка $(0,1)$ — числу $i$.

Вероятно, вы помните, что векторы на плоскости складываются по правилу параллелограмма или правилу треугольника (что в сущности одно и то же). В координатах, сложение векторов происходит покомпонентно — первая компонента первого вектора складывается с первой компонентой второго, втарая — со второй. Точно так же складываются комплексные числа. Поэтому сложение комплексных чисел работает в точности так же, как сложение векторов.

С умножением интереснее. На плоскости не существует обычного векторного умножения. (Вероятно, вы помните, что есть скалярное умножение, но оно на выходе возвращает не вектор, а число — скаляр; бывает ещё векторное умножение, но оно действует в трёхмерном пространстве, а не на плоскости.) А вот комплексные числа умножать можно. Есть ли у умножения какой-то геометрический смысл? Есть! Но сперва нужно поговорить про полярные координаты.

29.1.4Тригонометрическая форма записи комплексных чисел

Задать точку на плоскости можно по-разному. Можно — её координатами в декартовой системе, как мы это обычно делаем. А можно — в полярных координатах.

Возьмём некоторое направление — например, направление горизонтальной координатной оси от начала координат в сторону плюс бесконечности. Рассмотрим теперь какую-нибудь точку $P$. Она однозначно задаётся двумя числами: расстоянием до начала координат $O$ и углом $\phi$, который составляет $OP$ с нашим исходным направлением. Числа $r$ и $\phi$ называются полярными координатами точки $P$.

Полярные координаты иногда бывают удобнее декартовых. Например, чтобы задать единичную окружность, в декартовых координатах приходится вспоминать про теорему Пифагора и записывать уравнение $x^2+y^2=1$, а в полярных соответствующее уравнение выглядит гораздо проще: $r=1$.

Если заданы полярные координаты, восстановить декартовы легко. Если $r=1$, то $x=\cos \phi$ и $y=\sin \phi$ — это определение синуса и косинуса. Если $r\ne 1$, всю картинку нужно растянуть в $r$ раз, то есть умножить обе координаты на $r$. Получается такая штука:

Вернёмся к комплексным числам. Их тоже можно задавать в полярных координатах: Число $r$ называется модулем комплексного числа, оно равно расстоянию от точки $(Rez,Imz)$ до начала координат, а число $\phi$ называется аргументом. Обозначения такие: Таким образом, для любого $z$,

Умножение в тригонометрической форме. Посмотрим, как работает формула умножения комплексных чисел (29.1), если представлять их не в декартовых координатах, а в комплексных.

Теперь нужно внимательно вглядеться и напрячь память… это же формулы для косинуса и синуса суммы!Итак, при умножении комплексных чисел их модули умножаются, а аргументы складываются. В отличие от формулы (29.1), это правило реально запомнить, и оно имеет интересный геометрический смысл: умножение на комплексное число работает как поворот плоскости.

29.1.5Комплексное сопряжение и деление

Обсудим ещё две важные операции. Во-первых, с комплексным числом можно сделать такую штуку, которую нельзя сделать в вещественным числом: поменять знак мнимой части. Вернее, сделать её с вещественным числом можно, но вещественное число от этого не поменяется. Если же у комплексного числа есть ненулевая мнимая часть, её знак заменится на противоположный и получится другое комплексное число. Эта операция называется комплексным сопряжением и обозначается чертой:Геометрически комплексное сопряжение соответствует отражению плоскости относительно вещественной оси. Если применить комплексное сопряжение дважды, всё вернётся на место:

Рассмотрим теперь любое число $z$. Что будет, если умножить его на сопряженное?

Получается вещественное число — квадрат модуля $z$.

Научимся теперь делить комплексные числа. Для этого научимся для всякого $z\ne 0$ находить такое число $w$, что $wz=1$. То есть $w$ — обратное к $z$.

Начнём с равенства, которое мы только что вывели:

и поделим его на $|z{|}^2$, при условии, что $z\ne 0$ и следовательно $|z|\ne 0$:Итак, обратное к $z$ — это числоПочему такая запись лучше, чем просто $w=1/z$? Потому что в формуле выше мы делим на вещественное число $|z{|}^2$, а как умножать (и делить) на вещественные числа мы знаем — это можно делать покомпонентно (см. замечание 1). Можно записать операцию деления в обычных координатах: а можно и в полярных: взятие комплексного сопряжения меняет знак аргумента, а чтобы поделить комплексное число на вещественное, достаточно поделить его модуль:Ну а раз для всякого числа $z$ определено обратное к нему число $w$, то деление устроено как обычно — как умножение на обратное:

29.2Функции от комплексных чисел

29.2.1Возведение в квадрат

Мы начали с того, что добавили к обычным вещественным числам одно-единственное число $i$ — квадратный корень из минус единицы — и пообещали, что в получившейся системе чисел можно будет найти квадратный корень из любого числа. Давайте проверим, что это верно. Но сначала разберёмся, как действует возведение в квадрат.

Пусть $f\left(z\right)=z^2$, $z\in C$, то есть $f$ — это отобржаение из $C$ в $C$ — как говорят, комплекснозначная функция комплексного аргумента. К сожалению, представлять такие функции так, как мы привыкли, в виде графиком, практически невозможно — поскольку комплексное число соответствует двум вещественным, график такой функции пришлось бы рисовать в четыерёхмерном пространстве, которое очень трудно представить. Попробуем по-другому.

Запишем $z$ в тригонометрической форме:

Тогдапри возведении в квадрат модуль возводится в квадрат, а аргумент умножается на два.

Как действует это отображение? Для простоты рассмотрим случай, когда с радиусом ничего не происходит — а именно, пусть $r=1$. В этом случае наше квадратичное отображение просто удваивает аргумент, то есть отображает точку на единичной окружности с угловой координатой $\phi$ в точку $2\phi$.

Пусть точка $z$ постепенно обходит окружность от точки $\phi =0$ в положительном направлении (против часовой стрелки). Что происходит с $z^2$? Она также обходит окружность, но вдвое быстрее, см. анимацию на рис. 29.1. Когда $z$ сделает четверть оборота и окажется в точке с $\phi =\pi /2$ (то есть в точке $i$), её квадрат сделает полоборота и окажется в $(-1)$ — так и должно быть, мы знаем, что $i^2=-1$. Дальше $z$ будет преодолевать расстояние от $\phi =\pi /2$ до $\phi =\pi$, за это время $z^2$ преодолеет ещё полоборота и окажется в точке $1$. Всё логично: $(-1{)}^2=1$. Потом $z$ будет проходить вторую половину окружности, а $z^2$ — обходить всю окружность по второму разу. В частности, в тот момент, когда $z$ попадёт в точку $-i$ (что соответствует $\phi =3\pi /2$), её квадрат снова попадёт в $-1$. То есть не только $i^2=-1$, но и $(-i{)}^2=-1$ (что, конечно, мгновенно следует из правила «минус на минус даёт плюс», которое никто не отменял). Итак, полное прохождение окружности точкой $z$ соответствует двукратному прохождению окружности точкой $z^2$?

Что изменится, если теперь взять окружность не единичного радиуса, а какого-нибудь другого? Эта окружность всё равно перейдёт в окружность, но радиус образа будет квадратом радиуса прообраза. Если он был меньше 1, он ещё сильнее уменьшится. А если больше — увеличится. В остальном, никаких отличий нет: угол будет по-прежнему удваиваться, см. анимацию на рис. 29.2. Если поднапрячь воображение, можно представить себе, что делает это отображение с плоскостью целиком. Оно накладывает её саму на себя, накручивая два раза — так что у каждой точки, кроме нуля, есть ровно два прообраза. Это будет важно для дальнейшего.

29.2.2Квадратный корень

Попробуем теперь понять, как найти квадратный корень из комплексного числа. Это операция, обратная к возведению в квадрат. Чтобы возвести комплексное число в квадрат нужно его модуль возвести в квадрат, а аргумент удвоить. Значит, чтобы сделать обратную операцию, нужно извлечь корень из модуля (это всегда возможно, модуль — неотрицательное вещественное число) и поделить аргумент на два.

Звучит просто? Но не совсем.

Мы говорили о том, что аргумент не является определенным однозначно. Например, можно сказать, что аргумент числа $-1$ — это $\pi$, а можно сказать, что $3\pi$, а можно — что $5\pi$. И всё это будет верно, потому что эти аргументы отличаются ровно на $2\pi$ и задают одну и ту же точку.

Однако, когда мы их разделим пополам, вычисляя корень, мы можем получить разные точки. Действительно, если аргумент равняется $\pi$, я его делю пополам, и получаю аргумент $\pi /2$. Ему соответствует точка $i$. Если же я взял аргумент $3\pi$, после деления пополам я получу аргумент $3\pi /2$, что соответствует числу $(-i)$. То есть при делении аргумента пополам можно получить две разные точки.

Это, конечно, не должно нас удивлять. Анализируя отображение возведения в квадрат, мы выяснили, что оно не инъективно — а именно, у каждой точки, кроме нуля, есть ровно два прообраза. Поэтому логично, что обратное отображение не определено однозначно, и может принимать два разных значения.

Собственно, с такой же проблемой мы сталкивались, когда определяли обычный квадратный корень из неотрицательного вещественного числа. Однако, там мы легко вышли из этой ситуации, ограничив нашу функцию на неотрицательную полуось, или, иными словами, потребовав, чтобы квадратный корень (строго говоря, «арифметический квадратный корень») принимал только неотрицательные значения. Таким образом, мы получили корректно определенную, однозначную функцию, а в приложениях — например, в формуле корней квадратного уравнения — просто приписывали перед этим нашим «арифметическим квадратным корнем» знак $\pm$, который позволял не терять решений. Можем ли мы поступить так же с квадратным корнем из комплексного числа? Например, определить функцию «комплексный арифметический квадратный корень» таким образом, чтобы его значение всегда имело неотрицательную вещественную часть, или ещё как-то выбрав один из возможных корней и сняв таким образом неоднозначность? Давайте попробуем.

Возьмём снова точку $z$ на окружности, и пусть точка $w$ — это её квадратный корень. Пусть сначала $z=1$, то есть аргумент числа $z$ равен нулю или $2\pi$. Есть два возможных кандидата для значения корня — либо $w=1$, либо $w=-1$. Конечно, мы хотим, чтобы корень из единицы равнялся единице. Итак, пусть $w=1$ при $z=1$. Теперь начнём постепенно двигать $z$ по окружности. Мы также хотим, чтобы корень был непрерывной функцией, и когда мы немножко увеличим аргумент числа $z$, аргумент числа $w$ не должен измениться сильно. Это означает, что не может такого быть, чтобы мы только-только выехали из единицы, а $w$ вдруг стал близок к $(-1)$. Значит, если, например, аргумент числа $z$ равен $\pi /10$, то аргумент числа $w$ будет $\pi /20$, а не $\pi /20+\pi$. Пусть мы так постепенно сдвигая $z$, пройдём им полоборота по окружности, оказавшись в точке $1$. В это время $w$ проедет четверть оборота и окажется в точке $i$. Что ж, пока всё отлично — мы же знаем, что корень из минус единицы равен $i$, так и должно быть. Однако, пусть теперь $z$ едет дальше, и проезжает вторую половину окружности. В это время $w$ проедет вторую четвертинку и окажется в точке $-1$.

Стоп.

Но ведь точка $z$, проехав вторую половину окружности, сделал полный круг и вернулась в $1$. И мы только что сказали, что точка $w$, которая равна корню из $z$, при это оказалась равной $(-1)$. Хотя начинали мы с того, что принудительно положили корень из единицы равным единице. Как же так? Откуда вдруг противоречие?

Никакого содержательного противоречия тут на самом деле нет: $(-1{)}^2=1$ и в принципе число $(-1)$ может с тем же правом претендовать на звание квадратного корня из единицы, как и число $1$. Единственное, с чем возникло противоречие — это с нашим предположением, что мы можем по своем усмотрению однозначно выбрать, какому из двух возможных чисел этот корень равен. И вот это противоречие мы уже не сможем преодолеть — по крайней мере, сохраняя непрерывность корня.

В комплексных числах невозможно определить функцию $w=\sqrt{z}$ таким образом, чтобы она была непрерывной, но при этом однозначной — то есть так, как мы привыкли определять функции. Фактически, для всякого значения $z$, у $\sqrt{z}$ принимает два разных значения (отличающихся знаком), и, более того, нельзя сказать, какое из них «первое», а какое «второе» — в результате непрерывного обхода точкой $z$ вокруг нуля, эти значения поменяются местами.

Вот таким необычным образом могут выглядеть функции на множестве комплексных чисел.

29.2.3Экспонента

Давайте поговорим ещё про одну важную функцию — экспоненту. Для вещественнного числа $x$ мы определяли экспоненту как предели доказывали, что это определение эквивалентно такому определению через ряд (который впоследствии оказался рядом Тейлора):Ничто не мешает нам использовать одно из этих соотношений — например, второе — для определения экспоненты комплексного числа: достаточно уметь складывать числа, делить и возводить в степени. И мы всё это умеем!

Конечно, неплохо было бы доказать, что этот ряд сходится, но мы этого делать не будем. Вместо этого попробуем найти более явную формулу для экспоненты.

Для начала, рассмотрим случай чистого мнимого $z$, то есть $z=iy$. Посчитаем первые несколько степеней $z$, чтобы понять общий принцип: $$\begin{array}{cc}{z}^0& =1\\ z^1& =iy\\ z^2& =-y^2\\ z^3& =-i{y}^3\\ z^4& =y^4\\ z^5& =i{y}^5\end{array}$$ Итак, коэффициенты перед $y^k$ меняются таким образом: $1$, $i$, $-1$, $-i$, снова $1$ и дальше процесс повторяется циклически.

Запишем теперь первые члены ряда (29.4) и выделим вещественную и мнимую части:

Нет ли здесь чего-то вам знакомого? Ну конечно: ряд для вещественной части равен ряду Тейлора для косинуса, а для мнимой — синусу. Поскольку косинус и синус равны своим рядам Тейлора, мы получаем: иными словами — это число с единичным модулем и аргументом $y$. Таким образом, тригонометрическую запись комплексного числа (29.3) можно в сокращенной форме записывать так: (Если вы видите это впервые, я думаю, ваше ощущение примерно такое — а-а-а, откуда тут синусы, у нас же была экспонента?! А вот так. На самом деле, экспоненты и синус — это родственные функции. Но на вещественной оси этого совершенно не видно. Чтобы понять эту связь, нужны комплексные числа.)

Наконец, если у $z$ есть не только мнимая, но и действительная часть, экспонента определяется следующим естественным образом:

Если вы верите в то, что экспонента суммы равна произведению экспонент (а это можно доказать, анализируя ряд (29.4)), эта формула не должна казаться вам необычной.

29.2.4Логарифм

Итак, у нас есть экспонента. Как определить логарифм?

Посмотрим ещё раз на формулу (29.5). Её можно записать в таком виде. Пусть $e^{x+iy}=w$. Тогда

Теперь мы хотим наоборот, по $w$ найти $x+iy$. Это и будет наш логарифм.

Во-первых, легко найти $x$: раз $|w|=e^x$, числа $x$ и $|w|$ вещественны, и можно посчитать обычный вещественный логарифм:

Кажется, что $y$ найти ещё проще — это просто $Argw$. Однако, тут кроется подвох (он всегда кроется, когда мы рассматриваем аргумент): поскольку $Argw$ определен неоднозначно, $y$ тоже определен неоднозначно.

В комплексных числах экспонента не является инъективным отображением — что, впрочем, неудивительно, учитывая появление в ней синусов и косинусов. Более того, у каждой точки под действием экспоненты оказывается бесконечно много прообразов (а не два, как было в случае с возведением в квадрат). Поэтому каждое значение логарифма — это набор из бесконечного числа точек! И мы снова не можем выделить из них одну правильную.

где $Argw$ — это множество всевозможных значений аргумента $w$. Большие буквы в имени функции используются, чтобы подчеркнуть, что перед нами не совсем обычная функция — она принимает много разных значений.

29.3Фрактал Мандельброта

Теперь я могу рассказать про штуку, которая — в какой-то мере — привела меня в математику. Может быть, вам тоже понравится. Это фрактал Мандельброта.

Возьмём произвольное комлпексное число $c$ и рассмотрим такую последовательность комплексных чиспел $\left\{z_n\right\}$:

Например, $z_2=c$, $z_3=c^2+c$, $z_4=(c^2+c{)}^2+c$ и т.д.

К чему стремится эта последовательность? Если $c=0$, вся последовательность тождественно нулевая, и значит стремится к нулю. Если $c$ маленькое, наверное, последовательность колеблется где-то вблизи нуля или какой-то другой точки с небольшим модулем. Если $c$ большое, логично ожидать, что возведение в квадрат сделает его ещё больше и довольно быстро последовательность будет стремиться к бесконечности. Но как выглядит разделительная область между двумя режимами — когда последовательность ограничена и когда неограничена?

Давайте возьмём все точки комплексной плоскости, и раскрасим их в разные цвета. Если последовательность для выбранного значения $c$ не стремится к бесконечности — закрасим в чёрный. Если стремится — закрасим в разные цвета, в зависимости от того, как быстро она это делает (например, как быстро модуль становится больше десяти или даже двух — можно доказать, что если это произошло, то последовательность точно стремится к бесконечности). Что получится? Наверное, что-то вроде окружности? Или эллипс? Или что-то более сложное?

Оказывается, получается что-то неимоверно сложное — а именно, вот такая картинка.

Чтобы понять, насколько же она сложна, вы можете посмотреть, например, это видео (или любое другое по запросу mandelbrot zoom) — там нет ничего, кроме масштабирования этой картинки со всё большим увеличением — и там видно, что в ней бесконечно много всё более и более мелких деталей. (Подробнее о построении можно прочитать, например, здесь.)

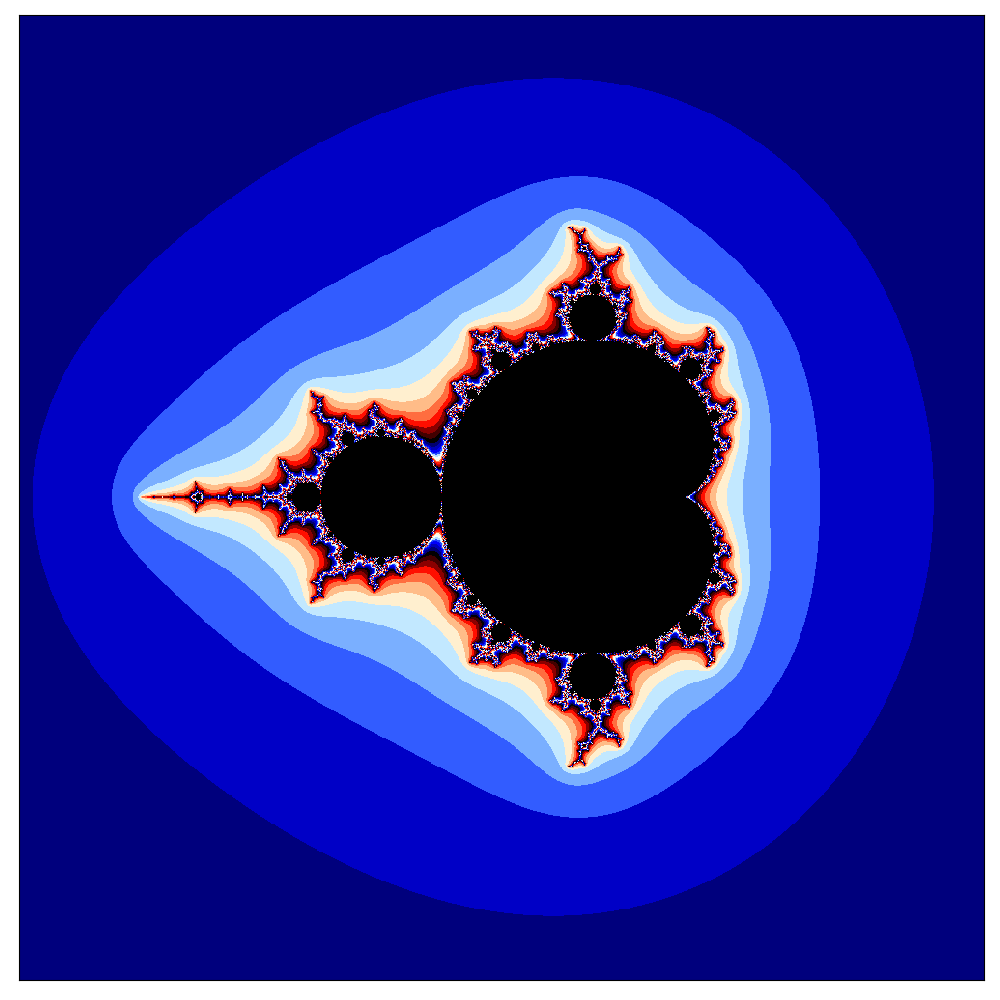
Множества с такими свойствами называются фракталами. Про фракталы у нас есть дополнительный листок с задачами — правда, множества Мандельброта там нет, потому что мы не обсуждали методов, которые позволили бы вам его исследовать — этим занимается отдельный раздел математики — так называемая голоморфная динамика.

Ну а пока можно просто посмотреть на картинку. Что самое удивительно — всю эту сложность породила одна очень простая формула: $f\left(z\right)=z^2+c$!

Пожалуй, трудно придумать лучшую иллюстрацию к величию и красоте математического мира — первые шаги в котором мы сделали в этом курсе.

---